Нам часто нужно из точек сделать меш, чтобы потом отрисовать его.
Для этой цели нужно использовать алгоритм триангуляции (например, вот этот). Вообще реализаций полно, так что не думаю что с этим будут проблемы.
Суть сводится к тому, чтобы на выходе получить треугольники (как следует из названия) из точек. А для создания мешки нам нужны вертексы (те самые точки) и индексы (как именно эти точки образуют треугольники).
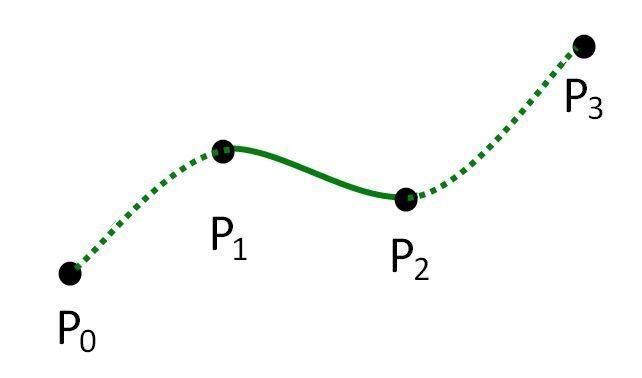
Это приведение к единичному размеру, при этом направление сохраняется. Обычно мы используем для этого v.normalized или v.Normalize(). Второй вариант будет немного быстрее первого, т.к. мы не создаем копию вектора, а изменяем существующий.
Но как оно работает внутри? Как нетрудно догадаться из определения нормализации, чтобы привести вектор к единичному - нам нужна его длина, а длина вектора - это корень по теореме Пифагора. Поэтому если вы по какой-то причине уже получили длину вектора, то просто поделите (ну поделите, ага https://t.me/unsafecsharp/150):
var inv_length = 1f / length; v.x *= inv_length; v.y *= inv_length;
И получите нормализованный вектор.
А то я часто встречаю примерно такой код в хот частях:
var length = v.magnitude; var n = v.normalized;
Хотя на деле проще было бы просто получить длину один раз и использовать ее дважды (ну или сделать свой метод для этого).
Давайте сначала разберемся что такое Lerp. Это линейная функция, которая задается двумя точками B и C (см изображение), а третье значение t - это как значение между 0 и 1, где 0 - это B, а 1 - это C.
Таким образом получается, что перемещение по линии - это и есть lerp или интерполяция. А вот LerpUnclamped - это экстраполяция, т.е. когда мы не обрезаем значение t до 0..1.
b + (c - b) * clamp01(t);
Т.е. по сути мы сначала сдвигаем сетку координат в ноль (c - b), а потом умножаем получившийся вектор на t, а после сдвигаем получившийся вектор назад.
С Unclamped мы просто не делаем операцию clamp, тем самым можем позволить результату выходить за границы b-c.
Надеюсь, что вы все в курсе, что операция деления выполняется намного медленнее операции умножения. Если нет, то имейте ввиду.
Я часто встречаю вот такой код:
a += b / 2f;
И мне все время хочется такой код написать так:
a += b * 0.5f;
Еще можно заменять по тому же принципу и любые другие константы. Но что делать, если у нас деление не на константу, а на x? Да все просто, делаем y = 1f / x и используем уже y.
Довольно простой вопрос, который решается банальной проверкой (v2.sqrMagnitude <= radius * radius). Мы такой вопрос часто задаем на собесах, но не только для того, чтобы выяснить считает ли человек через квадрат радиуса, а скорее для того, чтобы задать второй вопрос: "а в эллипс?". И вот на этом вопросе люди начинают сами себя закапывать. Кто-то придумывает несуществующие правила и теоремы, кто-то говорит, что мол "да я это не помню, там высшая математика, кому это вообще надо", ну а кто-то предлагает решение.
А самое интересное, что решение довольно простое, которое не требует никаких знаний и формул:
Изменяем Y проверяемой точки на фактор соотношения Rx к Ry, а дальше проверяем на попадание в радиус Rx. То есть мы вытягиваем эллипс таким образом, чтобы он стал кругом и считаем уже относительно круга.
Catmull rom - это такая кривая, для построения которой нужно знать 4 точки. Особенность заключается в том, что кривая будет проходить через все 4 точки.
На практике мы такое часто используем, т.к. для построения, например, Безье требуются тангенты, расчет которых иногда затруднителен.
Cross Product (векторное произведение) - по сути это способ нахождения нормали. Если у нас есть 2 вектора, то эти два вектора так или иначе образуют плоскость. Так вот Cross дает нам нормаль этой плоскости. Направление этой нормали (она же может смотреть как вверх, так и вниз) зависит от порядка этих векторов, т.е. если Cross(a, b), то нормаль смотрит вверх (как на картинке). Если же Cross(b, a), то нормаль будет смотреть вниз. Можно запомнить по так называемому правилу "правой руки":
Есть еще несколько свойств, которые мы получаем, подробнее можно почитать, например, в википедии или https://en.wikipedia.org/wiki/Cross_product.
Dot Product (скалярное произведение) - по сути способ определить угол между векторами. Формула довольно простая: x1*x2 + y1*y2 + z1*z2. То есть мы складываем произведения по каждой из осей. Окей, что нам это дает? Можно запомнить, что по сути это дает нам косинус угла между векторами, если они нормализованы (т.е. длина вектора единица), т.е. acos(dot(a, b)) дает нам угол.
Подробнее тут или https://en.wikipedia.org/wiki/Dot_product.
Да, это далеко не полный перечень того, что можно получить, но я же пытаюсь объяснить "простыми словами" :)
Довольно часто мы пишем в коде подобные штуки: direction * deltaTime * 2f
Фактически мы умножаем Vector direction на float и на какой-нибудь мультипликатор, например, 2. На самом деле лучше писать вот так:
direction * (deltaTime * 2f)
Т.к. в таком случае операций умножения для вектора будет одна вместо двух.
Я часто встречаю в различных проектах первый вариант при поиске ближайшей цели, например. Уж не знаю почему так получается, но, наверное, люди не особо вникают в то как это работает.
sqrMagnitude внутри: x*x + y*y + z*z
Vector3.Distance внутри: sqrt(x*x + y*y + z*z)
В sqrMagnitude по теореме Пифагора мы вычисляем расстояние между точками, тут все просто.
Но когда мы можем использовать sqrMagnitude? Самое банальное: проверка расстояния, когда каждая точка вычисляет расстояние одинаково. Получается, что корень считать нам нет никакой нужды, если нам нужно найти ближайший объект или, например, определить находится ли юнит в радиусе для выстрела.
Если вы хотите найти входит ли точка в любую фигуру, вам достаточно взять любое направление и посчитать количество пересечений с гранями этой фигуры. Если число четное - значит точка лежит вне фигуры, если нечетное - внутри.
OBB - это Oriented Bounding Box, это такой Rect с поворотом, но в 3D 🙂
Попробуйте ответить на этот вопрос до того, как посмотрите мое решение. Напишите в комменты свой вариант решения (просто описание алгоритма) хотя бы для 2D. Интересно было бы сравнить.
Мой вариант решения тут:
https://telegra.ph/Kak-poschitat-peresechenie-OBB-i-OBB-05-30